LAS SUCESIONES DE FIBONACCI
RESUMEN
En este presente
ensayo demostramos a las personas como surgen las sucesiones de Fibonacci y donde se encuentran, pues las encontramos
siempre en nuestra vida diaria por
ejemplo en las raíces de una planta, la reproducción de los conejos, en la
computación, en un caracol y en una radiografía de una mano, etc.
A lo largo del tiempo
Leonardo de Pisa, por su gran capacidad e interés por las matemáticas, construyó por primera vez la sucesión que lleva su nombre que son las
sucesiones de Fibonacci.
Besides applications of this sequence are in our daily
lives and we can see in: Human hand, the number of petals of a flower,
sunflowers spirals, the spirals of pineapples, the height of a human and height
of his navel, breeding rabbits the mona lisa and many other things.
INTRODUCCIÓN
Las sucesiones de Fibonacci nace gracias al fabuloso Leonardo de Pisa que es más conocido por Fibonacci, que
significa «hijo de Bonaccio», pues fue uno de los matemáticos más relevantes de
la Edad Media.
Además su gran deseo de poner en orden
todo cuánto había aprendido de aritmética y álgebra, y de brindar a sus colegas
comerciantes un potente sistema de cálculo, cuyas ventajas él había ya
experimentado; lo cual nace, en 1202, el Liber abaci, la primera
suma matemática de la Edad Media.
La sucesión de Fibonacci es una sucesión de números muy conocida y usada en matemáticas además es
una sucesión infinita que, empezando por la unidad, cada
uno de sus términos es la suma de los dos anteriores; resultando sorprendente que una construcción matemática
como esa aparezca recurrentemente en la naturaleza así como la distribución de
las hojas alrededor del tallo, la reproducción de los conejos o la disposición
de las semillas en numerosas flores y frutos se produce siguiendo secuencias
basadas exclusivamente en estos números.
Y lo podemos ver por una curiosa
sucesión de números:
0, 1, 1, 2,
3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584,
4181, 6765...,
Lo cual cada número se calcula sumando los
dos anteriores a él; es decir:
- El 2 se calcula sumando (1+1)
- Análogamente, el 3 es sólo (1+2),
- Y el 5 es (2+3),
- ¡y así sucesivamente sigue y sigue!
Es fácil ver que cada término es la suma de los dos
anteriores. Pero existe entre ellos otra relación curiosa, el cociente entre
cada término y el anterior se va acercando cada vez más a un número muy
especial, ya conocido por los griegos y aplicado en sus esculturas y sus
templos: el número áureo.  =1.618039....
=1.618039....
Pero los números de la sucesión de Fibonacci van a
sorprender a todos los biólogos.
Como muy bien nos enseña la filotaxia, las ramas y las
hojas de las plantas se distribuyen buscando siempre recibir el máximo de luz
para cada una de ellas. Por eso ninguna hoja nace justo en la vertical de la anterior es decir la distribución de las hojas alrededor
del tallo de las plantas se produce siguiendo secuencias basadas exclusivamente
en estos números.
Así mismo las sucesiones de Fibonacci cuentan con:
·
La ley de formación
·
Escribamos la serie de números que se obtienen
conforme van pasando los meses (supondremos que empezamos con cero conejos):
·
0, 1, 1, 2, 3, 5, 8, …
·
¿Somos capaces de escribir el siguiente número sin
recurrir al organigrama? No es difícil darse cuenta de que cada número de la
serie es la suma de los dos anteriores, de manera que, prolongándola un poco,
tendríamos
·
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,
610, 987, . . .
·
Existen varias fórmulas para encontrar el término
general, FN, de la Serie de Fibonacci, pero quizás
una de las más sorprendentes sea la que vienen dada por la expresión:
·


·
Y es sorprendente en la medida en que en
ella figura el término.
·

·
que es, ni más ni menos, que Φ = 1,
61803…, el llamado “número áureo”, la Divina Proporción, el número
mágico por excelencia, medida de la belleza y patrón del crecimiento en muchas
de las estructuras de los seres vivos.
Si construimos una tabla con unos
cuantos términos de la sucesión podremos observar que se puede obtener un
término cualquiera multiplicando el anterior por el número áureo.
v Propiedades
·
Cada término a partir del tercero, se obtiene sumando
los dos anteriores.
·
El cociente entre dos términos consecutivos de la
sucesión de Fibonacci se aproxima al número de oro ( = 1,618...).
·
Los números consecutivos de Fibonacci son primos entre
sí.
v Aplicaciones
·
Esta sucesión de números también aparece
en la Naturaleza, en el Arte (Arquitectura, Escultura, Pintura...) y en
la estructura de los mercados financieros de hoy día con numerosas aplicaciones
prácticas.
Además las aplicaciones de esta sucesión
se encuentran en nuestra vida diaria y
lo podemos ver en: La mano humana, el número de pétalos de una flor, las
espirales de los girasoles, las espirales de las piñas, la altura de un ser humano y la altura de su
ombligo, la cría de los conejos, la mona lisa y muchas otras cosas.
MÉTODOS Y MATERIALES
Para el presente
artículo utilizamos los siguientes métodos que son las sucesiones de Fibonacci
y el número áureo lo cual tomamos como modelo principal la reproducción de los
conejos y además agregamos otros más ejemplos como una radiografía de una mano, El número de espirales de un girasol
y en las conchas de los moluscos.
Los materiales que
utilizamos fueron imágenes, especialmente una donde se ve una reproducción de
conejos además accedimos a videos en “YouTube”, información en artículos
científicos en libros físicos y virtuales matemáticos, por Internet mediante el
buscador siendo las palabras claves sucesiones de Fibonacci, historia y aplicación
en la vida.
DESARROLLO
La sucesión de
Fibonacci es una secuencia de números enteros descubierta por matemáticos
hindúes hacia el año 1135 y descrita por primera vez en Europa gracias a
Fibonacci. Esta sucesión fue descrita por Fibonacci como la solución a un
problema de la cría de conejos. Muchas propiedades de la sucesión de Fibonacci
fueron descubiertas por Édouard Lucas, responsable de haberla denominado como
se la conoce en la actualidad; también es una sucesión numérica cuya naturaleza la puede comprender
cualquiera que tenga conocimientos de Aritmética Elemental. Sin embargo,
ninguna sucesión ha dado lugar a tantos teoremas y tantas aplicaciones
importantes como ésta.
La Sucesión de Fibonacci en la
naturaleza
La naturaleza nos brinda algunos
ejemplos de procreación sin necesidad de recurrir al incestuoso ejemplo de Fibonacci
como son los casos siguientes:
En los animales:
Tenemos
el caso de la reproducción de conejos y las espirales de los girasoles
El ejercicio de Fibonacci sobre la
reproducción de conejos nos pregunta cuántas parejas de conejos habrá en una
granja luego de 12 meses, si se coloca inicialmente una sola pareja y se parte
de las siguientes premisas:
- Los conejos alcanzan la madurez sexual a la edad de un mes.
- En cuanto alcanzan la madurez sexual los conejos se aparean y
siempre resulta preñada la hembra.
- El periodo de gestación de los conejos es de un mes.
- Los conejos no mueren.
- La hembra siempre da a luz una pareja de conejos de sexos opuestos.
- Los conejos tienen una moral y un instinto de variedad genética muy
relajados y se aparean entre parientes.
El proceso de crecimiento
de la población de conejos es mejor descrito con la siguiente ilustración.
Como se puede observar el número de
parejas de conejos por mes está determinado por la sucesión de Fibonacci. Así
que la respuesta al ejercicio acerca de cuántas parejas de conejos habrá luego
de un año, resulta ser el doceavo término de la sucesión: 144.
En
las plantas
Tenemos el ejemplo de los espirales de girasol
La
disposición regular de los órganos laterales de una planta (como las hojas en
un tallo o las florecillas en una flor compuesta), es un importante aspecto de
la forma de las plantas conocido como filotaxis.
El
área de la filotaxis está repleta de interesantes relaciones matemáticas, por
ejemplo, la extraordinaria predominancia de la sucesión de Fibonacci en el
número de espirales a lo largo de un patrón filotáctico; como modelo tenemos
las esferas de un girasol:
Un
modelo propuesto por H. Vogel para describir las estructuras espirales del
girasol está relacionado con problemas de empaquetamiento. La clave para este
modelo es el ángulo de Fibonacci.
entre dos brotes consecutivos es constante. El siguiente diagrama es una ilustración del modelo de Vogel.
La raíz cuadrada que
relaciona la distancia con el número de orden del brote tiene una simple
explicación geométrica. Suponiendo que los brotes tienen el mismo tamaño y que
el empaquetamiento es denso, el número de brotes que caben dentro de un disco
de radio r es proporcional al
área del disco, es decir que 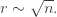
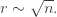
Es más difícil
explicar el ángulo de divergencia, que Vogel deduce a partir del supuesto de
que cada brote encaja en el mayor hueco que exista entre brotes anteriores. La
siguiente figura ilustra el crítico papel que desempeña el ángulo de
divergencia al generar patrones filotácticos en un disco cuando.
El
modelo de Vogel describe correctamente la disposición de los brotes en flores
reales. La característica más destacada son dos conjuntos de espirales
llamadas parastiquios, que girando el uno en sentido horario y el otro en
sentido anti horario, están compuestas de brotes adyacentes. El número de
espirales en cada parastiquio es siempre un término de la sucesión de
Fibonacci, oscilando desde 21y 34 para
una flor pequeña hasta 89 y 144 e
incluso 233 y 34 para
una flor grande. La margarita sintética de la siguiente imagen muestra espirales
horarias y 21 espirales
anti horarias.
Y
por último tenemos un ejemplo adicional sobre las hojas:
Las hojas nacen
siguiendo una espiral alrededor del tallo.
- En el reino vegetal aparece en la implantación espiral de las
semillas en ciertas variedades de girasol. Las escamas de una piña
aparecen en espiral alrededor del vértice. En el número de espirales
encontramos la sucesión de Fibonacci
En los seres humanos:
Tenemos La mano humana:
Sí. El largo de tus falanges también respeta la sucesión de Fibonacci.
¿Cómo es posible que el cociente de dos números de una secuencia
inventada por el hombre se relacionase con la belleza? La razón es
simple: la sucesión de Fibonacci está estrechamente emparentada con la
naturaleza.
En la vía láctea:
Tenemos un ejemplo de
las galaxias:
Las galaxias también creen en Fibonacci.
A una escala mucho
mayor, los brazos en espiral de las galaxias también se
acomodan según los números de Fibonacci. Sin dudas, es sorprendente la
relación que existe entre la matemática y la naturaleza, pero no se trata en absoluto de una
casualidad.
Otros contextos de Fibonacci
·
La sucesión de Fibonacci se
encuentra presente en muchos fenómenos naturales, pero no sólo en aquellos que
afectan a procesos de los seres vivos, sino también en procesos puramente
físicos como pueda ser los diferentes caminos que sigue un rayo de luz cuando es
reflejado.
·
Cuando miramos a través del cristal de
un escaparate podemos ver lo que hay en él si el interior está iluminado,
·
Pero si lo hacemos cuando el horario
comercial ha finalizado y las luces están apagadas, lo más probable es que
veamos nuestra imagen reflejada, ya que al haber más luz a un lado que al otro,
el cristal actúa como un espejo. Si nos acercamos lo suficiente podremos
observar una imagen doble, debida a una reflexión en la cara externa del
cristal y otra en la cara posterior, efecto que se conoce como reflexión
interna.
·
En base a este fenómeno se llevó a cabo
un experimento haciendo incidir oblicuamente un rayo de luz sobre láminas de
cristal planas puestas en contacto entre sí. Ya hemos visto lo que sucede en el
caso en que haya dos superficies. Si se trata de tres superficies puestas en
contacto el número de reflexiones posibles presenta la secuencia 1, 2, 3, 4,5.
·
Se ha demostrado (Leo Moser, Universidad
de Alberta) que, en el caso general, el número de trayectorias posibles sigue
una sucesión de Fibonacci.
CONCLUSIONES
Acosta
polo, Morelia
La Sucesión de Fibonacci ha
llegado a ser fuente inagotable de teoremas y problemas abiertos (conjeturas
que no se han conseguido demostrar), la mayoría de los cuales se circunscriben
a una parte de las Matemáticas llamada Teoría de Números. Además de presentar
un notable parentesco con uno de los números más míticos de las Matemáticas, el
número áureo, la sucesión
de Fibonacci es actualmente objeto de intensa investigación debido
a una multitud de aplicaciones, tanto teóricas como prácticas, que van desde la
posibilidad de encontrar máximos y mínimos de funciones de las que no se conoce
la derivada, hasta técnicas de recuperación de información digital.
Holguin
Merino Leidy
La Sucesión de Fibonacci
es muy importante en la en las matemáticas y se ve plasmada en la naturaleza,
en la reproducción de algunos de los animales, entre otras. Es sucesión de números muy conocida y usada en
matemáticas además es una sucesión infinita. La sucesión de Fibonacci la
tenemos gracias a Leonardo de Pisa.
Mendoza
Arteaga María
La sucesión inicia con 0 y 1, y a partir de ahí cada elemento
es la suma de los dos anteriores.
A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonado de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci.
Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono. En el cuerpo humano podemos decir que la cabeza es 1, el cuello, 1, los brazos (2), brazo, antebrazo y mano (3), luego los cinco dedos (5), es decir, la sucesión de Fibonacci hasta el 5.
A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonado de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci.
Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono. En el cuerpo humano podemos decir que la cabeza es 1, el cuello, 1, los brazos (2), brazo, antebrazo y mano (3), luego los cinco dedos (5), es decir, la sucesión de Fibonacci hasta el 5.
Linkografía:




